-
- Lesson roadmap
- Identifiers In Java
- Primitive Data Types In Java
- Declaring And Initializing Variables In Java
- Printing Variables Using The `system.out` Object
- Assignment Statements
- Math Operators
- Precedence Of Math Operators
- Assignment Operators
- Increment And Decrement Operators
- Summary
- Lab 3.1 Easter
- Lab 3.2 Changemachine
-
- Lesson roadmap
- Structured Programming
- Control Structures
- Algorithm Development And Psuedocode
- Relational Operators
- Logical Operators
- Precedence And Associativity Of Operators
- The If-else Statements
- Compound Statements
- Nested If-else Statements
- Conditional Operator
- Boolean Identifiers
- Switch Statements (optional)
- Summary
- Lab 8.1 Checkmail
- Lab 8.2 Happiness Detector
-
- Lesson roadmap
- The String Class
- String Constructors
- Object References
- The Null Value
- String Query Methods
- String Translation Methods
- Immutability Of Strings
- Comparing Strings
- Strings And Characters
- The Tostring Method
- String I/o
- Summary
- Lab 10.1 Iterative Reverse And Palindrome
- Lab 10.2 Shorthand
- Lab 10.3 Piglatin
- Lab 10.4 Carrental
- Lab 10.5 Romannumerals
- Lab 10.6 Complexuserinput
- Lab 10.7 Stringcraft
-
- Lesson roadmap
- Example Of An Array
- Array Declaration And Memory Allocation
- Application Of Arrays
- Arrays As Parameters
- Arrays And Algorithms
- Arrays And For-each Loops
- Summary
- Lab 16.1 Statistics
- Lab 16.2 Compact
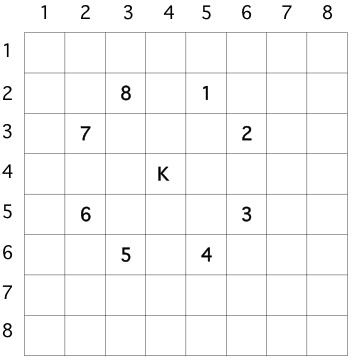
- Spider Solitaire Activity 1 To 3
- Spider Solitaire Activity 4 To 5
- Spider Solitaire Activity 6
- Spider Solitaire Activity 7 (final Version)
- S1 Final Review Problems
- Semester 1 Final Submission Form
Dark Mode
Outline