Order of Algorithms

1. The order of an algorithm is based on the number of steps that it takes to complete a task. Time is not a valid measuring stick because computers have different processing speeds. We want a method of comparing algorithms that is independent of the computing environment and the speed of the microprocessor.

2. Most algorithms solve problems involving an amount of data, N. The order of algorithms will be expressed as a function of N, the size of the data set.

3. The following chart summarizes the numerical relationships of common functions of N.

• The first column, N, is the number of items in a data set.

• The other four columns are mathematical functions based on the size of N. In computer science, we write this with a capital O (order) instead of the traditional F (function) of mathematics. This type of notation is the order of an algorithm, or Big O notation.

• The graph below, Order of Algorithms, gives a clearer sense of the relationships among the columns of numbers. Since the vertical axis represents the theoretical number of steps required by an algorithm to sort a list of N items, lines B and C represent more efficient algorithms than D and E. Today’s data sets can grow to enormous sizes, so algorithm designers are always searching for ways to reduce the number of steps, even on the fastest supercomputers.

  

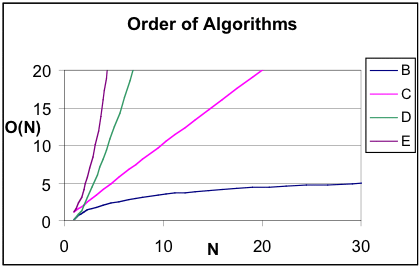
• You have already seen column E in an experimental sense when you counted the number of steps in the quadratic sorting algorithms. The relationship between columns A and E is quadratic - as the value of N increases, the other column increases as a function of N². The graph of column E is a portion of a parabola.