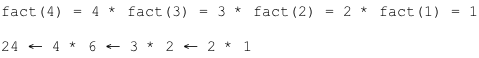Recursion

Recursion occurs when a method calls itself to solve another version of the same problem.

With each recursive call, the problem becomes simpler and moves towards a base case. A base case is when the solution to the problem can be calculated without another recursive call.

Recursion involves the internal use of a stack. A stack is a data abstraction that works like this: New data is "pushed," or added to the top of the stack. When information is removed from the stack it is "popped," or removed from the top of the stack. The recursive calls of a method will be stored on a stack and manipulated in a similar manner.

The problem of computing factorials is our first example of recursion. The factorial operation in mathematics is illustrated below.

1! = 1
2! = 2 * 1               or        2 * 1!
3! = 3 * 2 * 1           or        3 * 2!
4! = 4 * 3 * 2 *1        or        4 * 3!

Notice that each successive line can be solved in terms of the previous line. For example, 4! is equivalent to 4 * 3!

A recursive method to solve the factorial problem is given below. Notice the recursive call in the last line of the method. The method calls another implementation of itself to solve a smaller version of the problem.

int fact(int n){  
    // returns the value of n!  
    // precondition: n >= 1  
    if (n == 1){  
        return 1;  
    }else{
        return n * fact(n - 1);  
    }  
}

The base case is a fundamental situation where no further problem-solving is necessary. In the case of finding factorials, 1! is by definition 1. No further work is needed. Each recursive method must have at least one base case.

Suppose we call the method to solve fact(4). This will result in four calls of method fact.

When a recursive call is made, the current computation is temporarily suspended and placed on the stack with all its current information available for later use.

A completely new copy of the method is used to evaluate the recursive call. When that is completed, the value returned by the recursive call is used to complete the suspended computation. The suspended computation is removed from the stack and its work now proceeds.

When the base case is encountered, the recursion will now unwind and result in a final answer. The expressions below should be read from right to left.

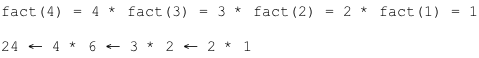
Figure 9.1 below diagrams what happens:

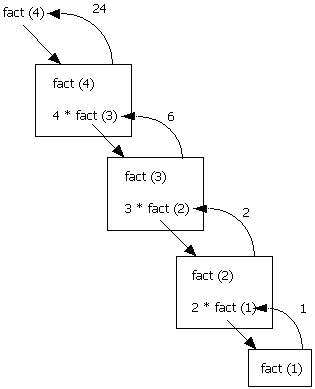
Figure 9.1 - Recursive Boxes

Each box represents a call of method fact. To solve fact(4) requires four calls of method fact.

Notice that when the recursive calls were made inside the else statement, the value fed to the recursive call was (n-1). This is where the problem is getting simpler with the eventual goal of solving 1!.