Lab 9.2 KochCurve

Background

You can create a number of line drawings by starting with a simple pattern that is recursively subdivided in parts, each of which is (at least approximately) a reduced-size copy of the whole. The results are related to mathematical objects called “fractals”, and so images generated in this manner are often called "fractal" images.

One example of a fractal curves is the “Koch curve” introduced by Swedish mathematician Helge von Koch in 1904. You can derive a Koch curve by beginning with the following basic four-segment piece:

Fig92

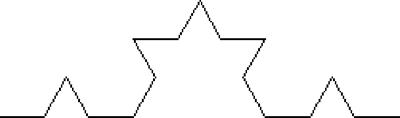
You then replace each line segment of the diagram with a smaller copy of itself.

Fig93

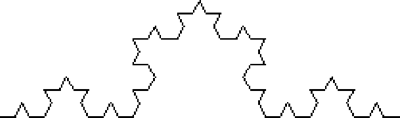
You again replace each line segment of the diagram with a smaller copy of the basic shape.

Fig94

Koch curves display an intricate beauty, as the number of levels of replacement increases. An even more remarkable figure can be created by joining three Koch curves as if they were the sides of a triangle. This figure is often referred to as a "Koch snowflake":

Fig95

The procedure for creating a Koch curve is usually recursive. At each level, we observe that a Koch curve is made up of four smaller Koch curves. This process can be described in the following pseudocode:

if level < 1 then
   Move forward length pixels
else
   Draw a k-1 level Koch curve with segments 1/3 the current length
   Turn left 60 degrees
   Draw a k-1 level Koch curve with segments 1/3 the current length
   Turn right 120 degrees
   Draw a k-1 level Koch curve with segments 1/3 the current length
   Turn left 60 degrees
   Draw a k-1 level Koch curve with segments 1/3 the current length

Instructions

1. Write a KochCurve program that uses DrawingTool and provides a drawKochCurve method for drawing Koch curves. Each drawKochCurve method can take the number of levels and an initial size as its parameters. Sample usage of the method to draw a 6 level Koch curve of length 300 would be:

   P3_Wang_Michael_KochCurve curve = new P3_Wang_Michael_KochCurve();
   curve.drawKochCurve(6, 300);
   

2. The constructor is up to you, but if anything only pass in a DrawingTool or SketchPad to use.

3. Have a drawKochCurve method that with (length, level) parameters that draws a regular Koch curve using the parameters.

4. Have a drawKochSnowflake method that draws three Koch curves connected to form a big triangle. That's how the snowflake is made. Parameters should be length and level.

5. Have a Driver that creates a KochCurve object and asks it to draw a Koch snowflake with a given length and level.

6. For fun, you can also create a Koch Antisnowflake. This isn't a lab requirement, but it's easy to do once you finish the main lab and it looks cool! A Koch Antisnowflake points "inward" instead of outward like a regular Koch Snowflake.

7. For an optional challenge, try to draw a Koch Snowflake interatively (using loops). The method header should be

   public void drawKochCurveIteratively(level, length)
   

   Submit both Your KochCurve and Driver classes.

You must Sign In to submit to this assignment